Question

What is the equation of this line?

y=−14x
y=−4x
y=14x
y = 4x

Answer 1

-4x

Explanation:

y is kind of like part of negative.

y=4x (kind of not really possible)

so add a negative sign.

which equals to -4x.

plus, the gragh shown below is a hint.

Answer 2

The equation for the line passing through the points (-4, 1), (0, 0), and (4, -1) is
`\[ y = -(1)/(4)x \]`.

To determine the equation of a line passing through the given coordinate points (-4, 1), (0, 0), and (4, -1), we can use the point-slope form of a linear equation, which is
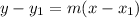`\(y - y_1 = m(x - x_1)\)`, where
`\((x_1, y_1)\)` is a point on the line, and m is the slope.

Let's calculate the slope using the given points (0, 0) and (4, -1):

`\[ \text{Slope, } m = \frac{{y_2 - y_1}}{{x_2 - x_1}} \]`

`\[ m = \frac{{-1 - 0}}{{4 - 0}} = -(1)/(4) \]`

Now that we have the slope, we can choose any of the given points to plug into the point-slope form. Let's use the point (0, 0):

`\[ y - 0 = -(1)/(4)(x - 0) \]`

Simplify:

`\[ y = -(1)/(4)x \]`

So, the correct equation of the line passing through the given coordinate points is
`\( y = -(1)/(4)x \)`.

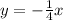The probable question may be:

What is the equation of this line?

coordinate points (-4, 1), (0, 0), and (4, -1)

y=−1/4x

y=−4x

y=1/4x

y = 4x