Question

In Texas, 30% of parolees from prison return to prison within 3 years.Suppose 15 prisoners are released from a Texas prison on parole. Assume that whether or not one prisoner returns to prison is independent of whether any of the others return to prison. Let the random variable X be the number of parolees out of 15 that return to prison within 3 years. What is the probability that more than 5 parolees out of 15 that return to prison within 3 years?

Answer 1

The probability that more than 5 parolees out of 15 that return to prison within 3 years is 0.2784.

Explanation:

The random variable X be the number of parolees that return to prison within 3 years.

The probability of occurrence of the random variable X is, p = 0.30.

A random sample of n = 15 prisoner are selected.

It is assumed that whether or not one prisoner returns to prison is independent of whether any of the others return to prison.

The random variable X follows a binomial distribution with parameters n = 15 and p = 0.30.

Compute the probability that more than 5 parolees out of 15 that return to prison within 3 years as follows:

`P(X>5)=1-P(X\leq 5)`

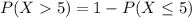
`=1-\sum\limits^(5)_(0){{15\choose x}(0.30^(x)(1-0.30)^(15-x)}\\\\=1-[0.00475+0.03052+0.09156+0.17004+0.21862+0.20613]\\\\=0.27838\\\\\approx 0.2784`

Thus, the probability that more than 5 parolees out of 15 that return to prison within 3 years is 0.2784.