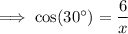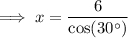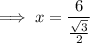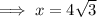Question

Please help with this problem about circles and tangents. solve for X.

Answer 1

As tangents from a single point to the circle are equal in measure

• AC=BC

ABC is isosceles

<A=60°

We know the radius hits any tangent on right angles

So

• <PAC=90°
• <PAD=90-60=30°

Now

• cosØ=Base/Hypotenuse
• cos30=6/x
• √3/2=6/x
• √3x=12
• x=12/√3

accurate value

• x=6.9

Answer 2

`x=4√(3)`

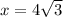
Explanation:

If two tangents to a circle meet at one exterior point, the tangent segments are congruent. Therefore, AC = BC

This means that ΔABC is an isosceles triangle and so
∠ABC = ∠BAC = 60°

The tangent of a circle is always perpendicular to the radius.

Therefore, ∠PAC = 90°

With this information, we can calculate ∠PAD:

⇒ ∠PAD + ∠BAC = ∠PAC

⇒ ∠PAD + 60° = 90°

⇒ ∠PAD = 90° - 60°

⇒ ∠PAD = 30°

We now have a side length and an angle of ΔPAD (shown in orange on the attached diagram). So using the cos trig ratio, we can calculate
`x`:

`\sf \cos(\theta)=(A)/(H)`

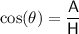
where:

• 
  `\theta` is the angle
• A is the side adjacent the angle
• H is the hypotenuse (the side opposite the right angle)

Given:

• 
  `\theta` = ∠PAD = 30°
• A = AD = 6
• H = AP =
  `x`

`\implies \cos(30^(\circ))=(6)/(x)`

`\implies x=(6)/(\cos(30^(\circ)))`

`\implies x=(6)/((√(3))/(2))`

`\implies x=4√(3)`