Answer:
Step One
Calculate the area of both the skating area and the spectator area.
Area = L * W
L = 4x
W = 4x
Area = 4x * 4x
Area = 16x^2
Step Two.
Find the radius of the semicircle. R = radius
From the diagram
R = The full length - the length given in the red shaded area.
R = 4x - 2x
R = 2x
Step Three
Find the area of the semicircle.
Area of a full circle = pi R^2
Area of a 1/2 circle =
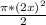
Area of a 1/2 circle =
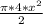
Area of a 1/2 circle =

Notice that the 2 in the denominator cancels in part with the 4 in the numerator.
Step Four
Find the area of the shaded area
Area of the shaded Area = Whole Area - Area of the Semi Circle.
Area of the shaded Area = 16x² -

The answer is the upper right corner choice I think