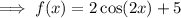Answer:
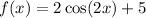
Explanation:
The cosine function is periodic, meaning it repeats forever.
Standard form of a cosine function:
f(x) = A cos(B(x + C)) + D
- A = amplitude (height from the mid-line to the peak)
- 2π/B = period (horizontal distance between consecutive peaks)
- C = phase shift (horizontal shift - positive is to the left)
- D = vertical shift
Given:
- Amplitude = 2 ⇒ A = 2
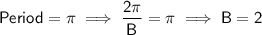
- mid-line = 5 ⇒ D = 5
Inputting the given values into the standard form: