Answer:
The length of the legs is 8.64cm and 14.64cm respectively
Explanation:
I've added an attachment to aid my explanation.
At different intervals, I'll be making reference to it.
Given
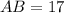
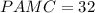
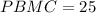
From the attachment, we have:
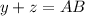
Since, M is the Midpoint
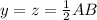
Substitute 17 for AB
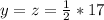
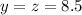
Also, from the attachment
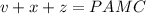
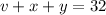
Substitute 8.5 for y

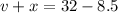
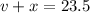 --------- (1)
--------- (1)
Also, from the attachment
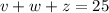
Substitute 8.5 for z
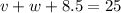

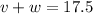 ----------- (2)
----------- (2)
Subtract (2) from (1)
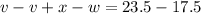
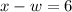
Make x the subject

Apply Pythagoras Theorem:
We have that:
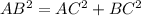
The above can be replaced with
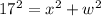 (see attachment)
(see attachment)

Substitute 6 + w for x
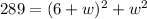
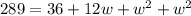
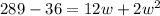
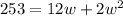
Reorder

Solve using quadratic equation:
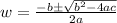
Where
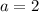
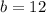

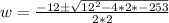
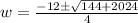
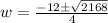

Split:
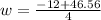 or
or

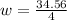 or
or
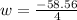
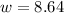 or
or
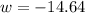
But length can't be negative
So:
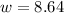
Recall that:

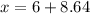
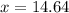
Hence, the length of the legs is 8.64cm and 14.64cm respectively