Question

In how many ways can a president, vice president, and secretary be chosen from a class of 20 girls and 30 boys if the president must be a girl and the vice president a boy?

Answer 1

Given:

Number of girls = 20

Number of boys = 30

The president must be a girl and the vice president a boy

To find:

Number of ways to choose a president, vice president, and secretary.

Solution:

The president must be a girl and the vice president a boy. So, out of three students 1 is girl and 1 is boy. Third student can be a girl or a boy.

Total number of ways = Selecting 2 boys and 1 girl + Selecting 1 boy and 2 girls

`=^(30)C_2* ^(20)C_1+^(30)C_1* ^(20)C_2`

`=(30!)/(2!(30-2)!)* (20!)/(1!(20-1)!)+(30!)/(1!(30-1)!)* (20!)/(2!(20-2)!)`

`=(30* 29* 28!)/(2* 1* 28!)* (20* 19!)/(19!)+(30* 29!)/(29!)* (20* 19* 18!)/(2* 1* 18!)`

`=(30* 29)/(2)* 20+20* (20* 19)/(2)`

`=8700+3800`

`=12500`

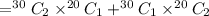
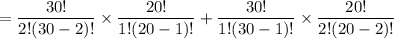
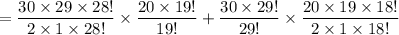
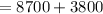
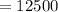
Therefore, the required number of ways is 12500.