Answer:
m∠2 = 53°
Explanation:
We will use two properties of a rhombus to solve this problem.
1). Opposite angles of a rhombus are equal.
2). Diagonals bisect the angles.
Since ∠JFG and ∠JHG are the opposite angles of the rhombus,
m∠JFG = m∠JHG
Since, diagonal FH bisect ∠JHG,
m∠FHJ = m∠GHF = m∠JFH = m∠GFH = 37°
In triangle JFH,
m∠FHJ + m∠JFH + m∠HJF = 180°
37° + 37° + m∠HJF = 180°
m∠HJF = 180 - 74
= 106°
Since, diagonal GJ bisects angle HJF,
m∠FJG =
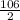 = 53°
= 53°
Therefore, m∠2 = 53°.