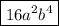Question

Click an item in the list or group of pictures at the bottom of the problem and, holding the button down, drag it into the correct position in the answer box. Release your mouse button when the item is place. If you change your mind, drag the item to the trashcan. Click the trashcan to clear all your answers. Find the GCF of the given polynomial. 16a^4b^4 + 32a^3b^5 - 48a^2b^6

Answer 1

`16a^2b^4`

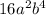
Explanation:

GCF= Greatest Common Factor

Given a polynomial, the GCF is the largest polynomial that will divide evenly into that polynomial.

The polynomial is

`16a^4b^4 + 32a^3b^5 - 48a^2b^6`

First, we find the GCF of the coefficients:

16, 32, 48

Since 32 and 48 are multiples of 16, 16 is the GCF of the coefficients.

Now we select all the repeating variables with their smallest exponent:

`a^4, a^3, a^2.\ GCF= a^2`

`b^4, b^5, b^6.\ GCF=b^4`

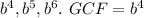
The GCF of the polynomial is

`\boxed{16a^2b^4}`