Question

Imagine a card game in which you have a 1 out of 10 chance of winning. If you win, you get $10. If you lose, you pay $2. What is the expected value of this game

Answer 1

Pay
`\$0.8`.

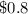Explanation:

Let
`X` denote the observed value of this game. Let positive values denote money received and negative values denote money paid.

There are two possible values for
`X`:

• 
  `X = 10` (receive
  `\$10`,) and
• 
  `X = -2` (pay
  `\$ 2`.)

The probability of each value is:

• 
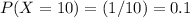  `P(X = 10) = (1 / 10) = 0.1` as given in the question.
• 
  `P(X = -2) = 1 - (1/10) = (9/10) = 0.9`.

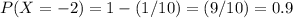The expected value of this game,
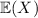`\mathbb{E}(X)`, is an average of the outcomes
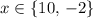`x \in \lbrace 10,\, -2\rbrace` weighted by the probability
`P(X = x)` of each outcome:

`\begin{aligned}\mathbb{E}(X) &= \sum\limits_(x) x\, P(X = x) \\ &= 10 * P(X = 10) + (-2) * P(X = -2) \\ &= 10 * (1)/(10) + (-2) * (9)/(10) \\ &= 1 - 1.8 \\ &= -0.8\end{aligned}`.

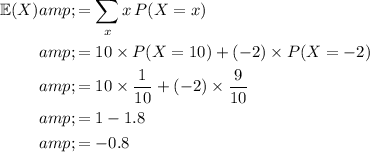The expected value of
`X` is
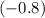`(-0.8)`, meaning that on average, playing this game would require paying
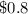`\$0.8`.