Answer:
Approximately
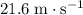 , assuming that the coefficient of kinetic friction between the tires and the ground stays the same.
, assuming that the coefficient of kinetic friction between the tires and the ground stays the same.
Step-by-step explanation:
Let
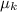 denote the coefficient of kinetic friction between the tires and the ground.
denote the coefficient of kinetic friction between the tires and the ground.
Let
 denote the mass of the truck. Let
denote the mass of the truck. Let
 denote the gravitational field strength. The weight of this truck would be
denote the gravitational field strength. The weight of this truck would be
 . Since the curve is flat, the magnitude of the normal force
. Since the curve is flat, the magnitude of the normal force
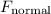 between the truck and the ground would also be
between the truck and the ground would also be
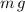 .
.
Let
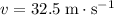 denote the speed at which the truck goes around the curve with a radius of
denote the speed at which the truck goes around the curve with a radius of
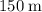 . The (horizontal) centripetal acceleration of the truck would be:
. The (horizontal) centripetal acceleration of the truck would be:
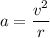 .
.
The horizontal net force on the truck (of mass
 ) would need to be exactly:
) would need to be exactly:
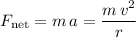 .
.
The friction between the tires of the truck and the ground is the only horizontal force on the truck. Thus, this friction would need to supply the entirety of this horizontal net force:
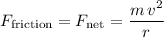 .
.
Notice that increasing
 would require an increase in the kinetic friction between the truck,
would require an increase in the kinetic friction between the truck,
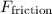 . However, since
. However, since
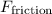 is at most
is at most
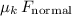 (which is equal to
(which is equal to
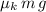 ):
):
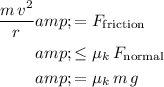 .
.
Therefore, when the radius of the curve is
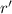 , the maximum velocity of this truck would be:
, the maximum velocity of this truck would be:
 .
.
Likewise, it is possible to express
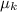 in terms of
in terms of
 ,
,
 , and max speed
, and max speed
 :
:
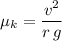 .
.
Substitute this expression for
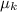 back into the expression for
back into the expression for
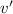 :
:
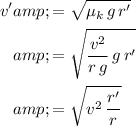 .
.
Given that
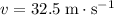 ,
,
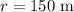 , and
, and
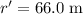 :
:
 .
.