OPTIONS:
*The slope of the graph of the table is 1 more than the slope of the graph of the equation.
*The slope of the graph of the table is 2 more than the slope of the graph of the equation.
*The slope of the graph of the equation is 2 more than the slope of the graph of the table.
*The slope of the graph of the equation is 1 more than the slope of the graph of the table.
Answer:
The slope of the graph of the equation is 1 more than the slope of the graph of the table.
Explanation:
The slope in the equation of the function, y = 3x + 2, is identified as 3.
We know this because, the equation for the function was given in the slope-intercept form, y = mx + b, where m represents the slope.
Therefore, the slope of the function is 3.
The slope of the function represented by the table of values can be calculated using any two given pairs on the table.
Using (1, 6) and (3, 10):
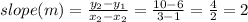
Slope of the function represented by the table of values is 2.
Therefore, comparing the slope of both functions, we can conclude that:
✅"The slope of the graph of the equation is 1 more than the slope of the graph of the table."