Question

Use the three functions shown. 1. f(x)=x² II. f(x)=√x III. f(x) = ln x For which of the functions, if any, is a trapezoidal approximation for the area under the curve y = f(x) over the interval [1, 4] with 3 equal subintervals less than the midpoint approximation? none of the functions O I only II and III only all of the functions​

Answer 1

II and III only

We split up the integration interval [1, 4] into 3 equally-spaced subintervals of length (4 - 1)/3 = 1 :

[1, 2], [2, 3], [3, 4]

The area over each subinterval [L, R] is either approximated by a trapezoid, whose area will be

1 • (f(L) + f(R))/2

or by a rectangle with height f((L + R)/2) and hence area

1 • f((L + R)/2)

For f(x) = x², the area under f(x) over [1, 4] is approximated by

• using trapezoids (T) :

`\displaystyle \int_1^4 x^2 \, dx \approx (4-1)/(2*3) (1^2 + 2*2^2 + 2*3^2 + 4^2) = \frac{43}2 = \frac{86}4`

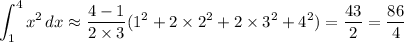
• using midpoints (M) :

`\displaystyle \int_1^4 x^2 \, dx \approx \frac{4-1}3 \left(\left(\frac32\right)^2 + \left(\frac52\right)^2 + \left(\frac72\right)^2\right) = \frac{83}4`

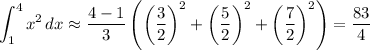
so T > M. (This eliminates "I only" and "all of the functions".)

For f(x) = √x, the area is approximated by

• T :

`\displaystyle \int_1^4 \sqrt x \, dx \approx (4-1)/(2*3) (\sqrt1 + 2\sqrt2 + 2\sqrt3 + \sqrt4) \approx 4.646`

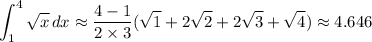
• M :

`\displaystyle \int_1^4 \sqrt x\, dx \approx \frac{4-1}3 \left(√(\frac32) + √(\frac52) + √(\frac72)\right) \approx 4.677`

so T < M. (This eliminates "none of the functions".)