Question

The table below represents a linear function f(x) and the equation represents a function g(x):

Part A: Write a sentence to compare the slope of the two functions and show the steps you used to determine the slope of f(x) and g(x). (6 points)

Part B: Which function has a greater y-intercept? Justify your answer. (4 points)

Answer 1

Slope of f(x) is greater than slope of g(x)

g(x) has a greater y intercept

Explanation:

Given

f(x) table

`g(x) = 2x + 6`

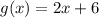
Solving (a):

First, we determine the slope of f(x).

From the table, we take any two corresponding values of x and f(x).

Represent f(x) with y

`(x_1,y_1) = (-1.-12)`

`(x_2,y_2) = (0.-6)`

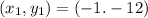
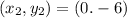
The slope (m) is calculated as thus

`m = (y_2 - y_1)/(x_2 - x_1)`

`m = (-6 - (-12))/(0 - (-1))`

`m = (-6 +12)/(0 +1)`

`m = (6)/(1)`

`m = 6`

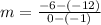
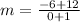
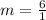
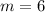
Represent this with m1

`m_1 = 6`

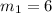
Calculating the slope of g(x).

The general form of an equation is
`y = mx + b`

Where m represents the slope.

We have that:

`g(x) = 2x + 6`

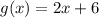
By comparing
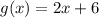`g(x) = 2x + 6` with
`y = mx + b`

`m = 2`

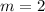
Represent this with m2

`m_2 = 2`

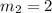
Comparing both slope, we can say that:

f(x) has a greater than slope of g(x)

Another comparison is that:

Slope of f(x) is 3 times the slope of g(x)

Solving (b): Function with greater y intercept.

The general form of an equation is
`y = mx + b`

Where b represents the y intercept.

First, we need to determine the equation of f(x) using:

`y - y_1 = m(x - x_1)`

Recall that, from the table of f(x):

`(x_1,y_1) = (-1.-12)`

`(x_2,y_2) = (0.-6)`

`m_1 = 6`

So:

`y - y_1 = m(x - x_1)`

`y - (-12) = 6(x - (-1))`

`y + 12 = 6(x +1)`

`y + 12 = 6x +6`

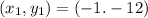
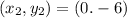
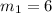
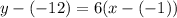
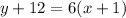
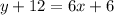
Solve for y

`y = 6x + 6 - 12`

`y = 6x - 6`

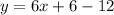
By comparing this with
`y = mx + b`, the y intercept of f(x) is -6

For g(x), we have:

`g(x) = 2x + 6`

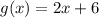
By comparing this with
`y = mx + b`, the y intercept of g(x) is 6

Comparing the y intercepts of both functions, g(x) has a greater y intercept because
`6 > -6`