Question

Rachelle has $4.75 in nickels, dimes, and quarters. If she has four more nickels than dimes and twice as many quarters as dimes, how many of each kind of coin does she have?

Answer 1

Given:

Total amount Rachelle has = $4.75

She has four more nickels than dimes and twice as many quarters as dimes.

To find:

The number of each kind of coin.

Solution:

Let the number of dimes be x. So,

Number of nickels = x+4

Number of quarters = 2x

We know that, 1 nickel = $0.05, 1 dime = $0.10 and 1 quarter = $0.25.

Total amount Rachelle has = $4.75.

`0.05(x+4)+0.10x+0.25(2x)=4.75`

`0.05x+0.20+0.10x+0.50x=4.75`

`0.65x+0.20=4.75`

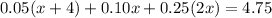
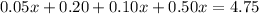
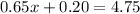
Subtract both sides by 0.20.

`0.65x=4.75-0.20`

`0.65x=4.55`

Divide both sides by 0.65.

`x=(4.55)/(0.65)`

`x=7`

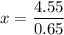
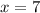
Now,

Number of dimes = 7

Number of nickels = 7+4 = 11

Number of quarters = 2(7) = 14

Therefore, the number of dimes, nickels and quarters are 7, 11 and 14 respectively.