Question

A 20Kg box is pushed across the floor at a constant velocity with a force of 200N. What is the

kinetic friction coefficient between the box and the floor?

Answer 1

The kinetic coefficient of friction between the box and the floor is 1.020.

Step-by-step explanation:

Let suppose that box is on horizontal ground. According to the Newton's Laws, an object has a net acceleration of zero when either is at rest or moves at constant velocity. Friction is a reaction to the external force that moves the box. Hence, the equation of equilibrium for the 20-Kg box is:

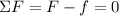`\Sigma F = F-f = 0` (Eq. 1)

Where:

`F` - External force, measured in newtons.

`f` - Friction force, measured in newtons.

If we know that
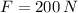`F = 200\,N`, then the magnitude of the kinetic friction force is:

`f = F`

`f = 200\,N`

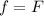
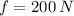
In addition, friction force is represented by the following formula:

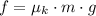`f = \mu_(k)\cdot m\cdot g` (Eq. 2)

Where:

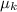`\mu_(k)` - Kinetic coefficient of friction, dimensionless.

`m` - Mass, measured in kilograms.

`g` - Gravitational acceleration, measured in meters per square second.

Now we clear the kinetic coefficient of friction:

`\mu_(k) = (f)/(m\cdot g)`

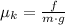
If we know that
`f = 200\,N`,
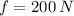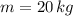`m = 20\,kg` and
`g = 9.807\,(m)/(s^(2))`, then the kinetic coefficient of friction is:

`\mu_(k) = (200\,N)/((20\,kg)\cdot \left(9.807\,(m)/(s^(2)) \right))`

`\mu_(k) = 1.020`

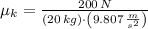
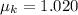
The kinetic coefficient of friction between the box and the floor is 1.020.