Answer:
The length of the segment F'G' is 7.
Explanation:
From Linear Algebra we define reflection across the y-axis as follows:
 ,
,
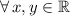 (Eq. 1)
(Eq. 1)
In addition, we get this translation formula from the statement of the problem:
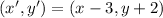 ,
,
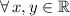 (Eq. 2)
(Eq. 2)
Where:
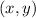 - Original point, dimensionless.
- Original point, dimensionless.
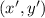 - Transformed point, dimensionless.
- Transformed point, dimensionless.
If we know that
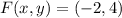 and
and
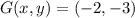 , then we proceed to make all needed operations:
, then we proceed to make all needed operations:
Translation
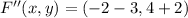
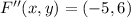

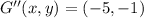
Reflection
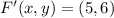
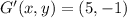
Lastly, we calculate the length of the segment F'G' by Pythagorean Theorem:
![F'G' = \sqrt{(5-5)^(2)+[(-1)-6]^(2)}](https://img.qammunity.org/2021/formulas/mathematics/high-school/l7j9u2oa8rdbwfcn8be7jp5x75zs9dd0wt.png)

The length of the segment F'G' is 7.