Question

A total of $44,000 is invested in two municipal bonds that pay 5.75% and 6.25% simple intrest. The investor wants an annual interest income of $2,680. What is the most that can be invested in the 5.75% bond?

Answer 1

$22333.33

Explanation:

The total amount to be invested is $44,000.

Let x be the amount that can be invested in the 5.75% bond.

So, the annual simple interest for this amount is

`I_1=x * (5.75)/(100)=(5.75x)/(100).`

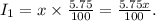
The remaining amount that can be invested in the 6.25% bond is 44000-x.

The annual simple interest for this amount is

`I_2=(44000-x) * (6.25)/(100)=(6.25x)/(100).`

As the investor wants an annual interest income of $2,680, so

`I_1 + I_2 = 2,680`

`\Rightarrow (5.75x)/(100) + (6.25x)/(100) = 2680`

`\Rightarrow (5.75x+6.25x)/(100)= 2680`

`\Rightarrow (12x)/(100)= 2680`

`\Rightarrow x= \frac {2680*100}{12}`

`\Rightarrow x=22333.33`

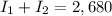
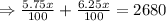
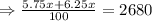
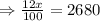
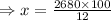
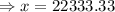
Hence, the amount to be invested at a rate of 5.75% is $22333.33.