Question

For a given set of rectangles, the length is inversely proportional to the width. In one of these rectangles, the length is 58 and the width is 3. For this set of rectangles, calculate the width of a rectangle whose length is 2.

Answer 1

The width is 87

Explanation:

Given

Represent Length with L and Width with W

Variation: Inverse Proportion

`L \alpha (1)/(W)`

`L = 58; W = 3`

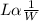
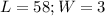
Required

Solve for W when L = 2

First, we need to determine the constant of variation

`L \alpha (1)/(W)`

`L = (k)/(W)`

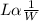
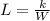
Where

k = constant of variation

Substitute the following values:
`L = 58; W = 3`

`58 = (k)/(3)`

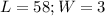
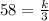
Solve for k

`k = 58 * 3`

`k = 174`

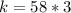
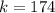
To solve for W when L = 2, we simply substitute values for L and K in the expression
`L = (k)/(W)`

`2 = (174)/(W)`

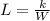
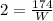
Solve for W

`2 * W = 174`

`2 W = 174`

`W = 174/2`

`W = 87`

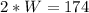
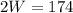
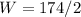
Hence, the width is 87