Question

(a) The lower yield point for an iron that has an average grain diameter of 1 x 10-2 mm is 230 MPa. At a grain diameter of 6 x 10-3 mm, the yield point increases to 275 MPa. At what grain diameter will the lower yield point be 310 MPa? (b) Predict the yield strength of the iron when the average grain diameter is 8.0 x 10-3 mm.

Answer 1

The answer is "
`4.35 * 10^(-3)\ mm` and 157.5 MPa".

Step-by-step explanation:

In point A:

The strength of its products with both the grain dimension is linked to this problem. This formula also for grain diameter of 310 MPA is represented as its low yield point

`y = yo + (k)/(√(x))`

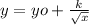
Here y is MPa is low yield point, x is mm grain size, and k becomes proportionality constant.

Replacing the equation for each condition:

`y = y_o + \frac{k}{\sqrt{(1 * 10^(-2))}}\\\\\ \ \ \ \ \ \ 230 = yo + 10k\\\\ y = yo + \frac{k}{\sqrt{(6* 10^(-3))}}\\\\275 = yo + 12.90k`

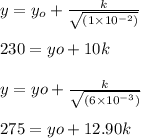
People can get yo = 275 MPa with both equations and k= 15.5 Mpa
`mm^{(1)/(2)}`.

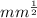To substitute the answer,

`310 = 275 + ((15.5))/(√(x))\\\\x = 0.00435 \ mm = 4.35 * 10^(-3)\ mm`

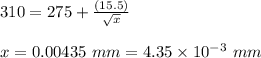
In point b:

The equation is
`\sigma y = \sigma 0 + k y d^{(1)/(2)}`

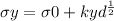
equation is:

`75 = \sigma o+4 ky \\\\175 = \sigma o+12 ky\\\\ky = 12.5 MPa (mm)^{(1)/(2)} \\\\ \sigma 0 = 25 MPa\\\\d= 8.9 * 10^(-3)\\\\d^{- (1)/(2)} =10.6 mm^{-(1)/(2)}\\`

by putting the above value in the formula we get the
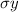`\sigma y` value that is= 157.5 MPa