Answer:
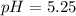
Step-by-step explanation:
Hello.
In this case, since the volume of the aniline (Kb = 7.41x10⁻¹⁰) is 160.0mL, its concentration 0.3403 M and the HNO3 solution is 0.0501 M, we can first compute the employed volume of the acid via:
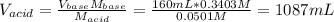
Because at the equivalence point, the moles of acid equals the moles of base, which causes that at equilibrium the mayor species are NO₃⁻, C₆H₅NH₃⁺ and H₂O which means that the following ionization occurs:
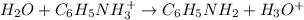
And the pH at the equivalence point is lower than 7 due to the presence of the hydronium ion, that is why we use Ka rather than Kb. Next, we write the equilibrium expression:
![K_a=([C_6H_5NH_2][H_3O^+])/([C_6H_5NH_3^+])](https://img.qammunity.org/2021/formulas/chemistry/college/mywypwky0f63w28vksu9as5oiwjss5pq6c.png)
Which based on the ICE chart, knowing that Kw=Ka*Kb and Kb is so small, we write:
![Ka=(K_w)/(K_b)=(1x10^-14)/(1.35x10^(-5))=7.41x10^(-10)\\\\7.41x10^(-10)=(x*x)/([C_6H_5NH_3^+]_0)](https://img.qammunity.org/2021/formulas/chemistry/college/hy9y9k4p039tmc671vv1p8sl7eqvzgspxs.png)
Whereas the initial concentration of C₆H₅NH₃⁺ is:
![[C_6H_5NH_3^+]_0=(0.16L*0.3403mol/L)/((1.087+0.16)L) =0.0437M](https://img.qammunity.org/2021/formulas/chemistry/college/lj3d6m5wqum5kwmnpov7knkdmonu91qrby.png)
Therefore, the concentration of hydronium un solution which equals
 is:
is:
![[H_3O^+]=x=\sqrt{7.41x10^(-10)*0.0437M}=5.69x10^(-6)M](https://img.qammunity.org/2021/formulas/chemistry/college/kwv32pvvgn9aa605mb9ak9u9138mhqjh7y.png)
Thus the pH is:
![pH=-log([H_3O^+])=-log(5.67x10^(-6))\\\\pH=5.25](https://img.qammunity.org/2021/formulas/chemistry/college/y3viifri8xmek73p4ueqxkp8rqrwm3c368.png)
Best regards!