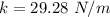Question

A cart of mass 0.68 kg is attached to one end of of a spring and placed on a low-friction track, inclined at an angle of 61.5 degrees with respect to the horizontal. The cart is found to be in equilibrium when the spring is stretched to a total length of 52.0 cm. Given that the rest length for the spring is 12 cm, what is the spring constant for the spring

Answer 1

The value is
`k = 29.28 \ N / m`

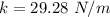
Step-by-step explanation:

From the question we are told that

The mass of the cart is m = 0.68 kg

The angle of inclination is
`\theta = 61.5^o`

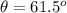
The length of the spring when the cart is a equilibrium is
`d = 52.0 \ cm = 0.52 \ m`

The length of the spring when at rest is
`d_r = 12 \ cm = 0.12 \ m`

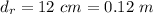
Generally the weight of the cart is mathematically represented as

`W_c = m * g * sin (\theta )`

=>
`W_c = 0.68 * 9.8 * sin (61.5 )`

=>
`W_c = 5.856 \ N`

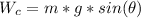
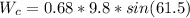
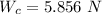
Generally the force applied on the spring by the weight of the cart is mathematically represented as

`F = (1)/(2) * k * (d - d_r )`

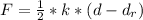
So at equilibrium

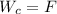
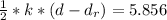
`W_c = F`

=>
`(1)/(2) * k * (d - d_r ) = 5.856`

=>
`0.5 * k * (0.52 - 0.12 ) = 5.856`

=>
`k = 29.28 \ N / m`