Answer:
a
The new frequency is 2.0 Hz
b
The new amplitude is
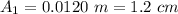
Step-by-step explanation:
From the question we are told that
The mass of the block is

The first amplitude is
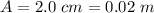
The frequency is
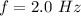
The force exerted is F = 20 N
The duration of the force is
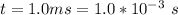
Generally the impulse is mathematically represented as

=>

=>
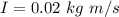
Generally the initial angular speed of the block is mathematically represented as
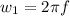
=>
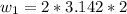
=>
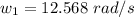
Generally the linear velocity of the block at the equilibrium position before the impact is mathematically represented as
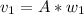
=>
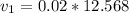
=>

Generally the change in velocity after that impact of the force is mathematically represented as
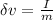
=>
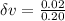
=>
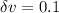
Generally the linear velocity of the block at the equilibrium position after the impact is mathematically represented as
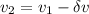
=>
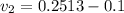
=>

This can also be mathematically represented as
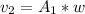
=>
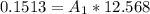
=>
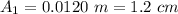
Generally given that the angular velocity does not change , it then implies that the frequency remains 2.0 Hz