Answer:
The points (4,11), (6,14), (30,50) lie on the line joining the points (0,5) and (2,8).
Explanation:
The equation of the line passing through two points
 and
and
 is
is
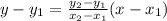
So, the equation of the line passing through two points (0,5) and ( 2, 8 ) is
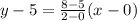
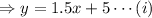
For the point (4,11), pout x=4 in equation (i), we have
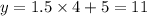 , which is given y coordinate, hence this point (4,11) lies on the line.
, which is given y coordinate, hence this point (4,11) lies on the line.
For the point (5,10), pout x=5 in equation (i), we have
 which is not the given y coordinate, hence the point (5,10) doesn't lie on the line.
which is not the given y coordinate, hence the point (5,10) doesn't lie on the line.
For the point (6,14), pout x=6 in equation (i), we have
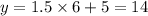 , which is the given y coordinate, hence the point (6,14) lies on the line.
, which is the given y coordinate, hence the point (6,14) lies on the line.
For the point (30,50), pout x=30 in equation (i), we have
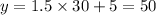 , which is the given y coordinate, hence the point (30,50) lies on the line.
, which is the given y coordinate, hence the point (30,50) lies on the line.
For the point (40,60), pout x=40 in equation (i), we have
 , which is not the given y coordinate, hence the point (40,60) doesn't lie on the line.
, which is not the given y coordinate, hence the point (40,60) doesn't lie on the line.
Hence, the points (4,11), (6,14), (30,50) lie on the line joining the points (0,5) and (2,8).