Complete Question
poll indicates that 47% of a country's adults favor a ban on assault weapons. Suppose 330 adults in a certain region are randomly surveyed and 161 say they favor a ban. Based on this sample, test using alpha = 0.025 whether the proportion of the region's residents who favor the ban is different from the proportion given in the poll for the country as a whole. Report the p-value for this hypothesis test.
Identify the null and alternative hypotheses for this test. Let p be the population proportion of the region's residents who favor a ban on assault weapons.
A.

B

C
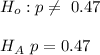
D
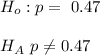
Perform the test using a normal approximation. Identify the test statistic. (Round to two decimal places as needed.)
Identify the p-value. (Round to three decimal places as needed.)
State the conclusion for this hypothesis test.
Answer:
The correct option is D
The test statistics is
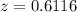
The p-value
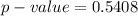
The conclusion
There no sufficient evidence to state that the proportion of the region's residents who favor the ban is different from the proportion given in the poll for the country as a whole.
Explanation:
From the question we are told that
The population proportion is p = 0.47
The sample size is n = 330
The number that favor the ban is k= 161
The level of significance is

The null hypothesis is
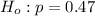
The alternative hypothesis is
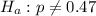
Generally sample proportion is mathematically represented as
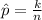
=>
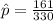
=>
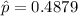
Generally the test statistics is mathematically represented as
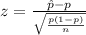
=>
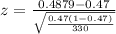
=>
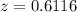
From the z table the area under the normal curve to the right corresponding to 0.6116 is
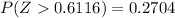
given that is a two tailed test the p-value is mathematically represented as
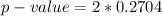
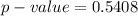
From the values obtained we see that
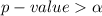 so
so
The decision rule is
Fail to reject the null hypothesis
The conclusion
There no sufficient evidence to state that the proportion of the region's residents who favor the ban is different from the proportion given in the poll for the country as a whole