The question displayed below shows the missing information which therefore completes the question.
An organic compound contains C, H, N and O. Combustion of 0.1023 g of the compound in excess oxygen yielded 0.2587 g of CO2 and 0.0861 g of H2O. A sample of 0.4831 g of the compound was analyzed for nitrogen by the Dumas method. The compound is first reacted by passage over hot: The product gas is then passed through a concentrated solution of to remove the. After passage through the solution, the gas contains and is saturated with water vapor. At STP, 38.9 mL of dry N2 was obtained. In a third experiment, the density of the compound as a gas was found to be 2.86 g/L at 127°C and 256 torr. What are the empirical and molecular formulas of the compound? (Enter the elements in the order: C, H, N, O.)
Answer:
the empirical formula =
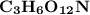
the molecular formula =
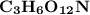
Step-by-step explanation:
From the given information:
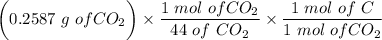
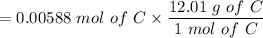
= 0.0706g of C
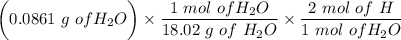
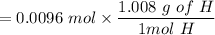
0.0097g of H
Given that N2 at STP = 1 atm, 273 K and V = 0.0389 L
PV = nRT
n = PV/RT
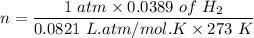
n = 0.00173 mol of N2
The oxygen in the sample = The total grams in sample - gram in H - gram in C
The oxygen in the sample = 0.1023 g - 0.0097 g - 0.706 g
The oxygen in the sample = 0.022 g of O
The number of moles of
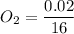
= 0.001375 mol of O
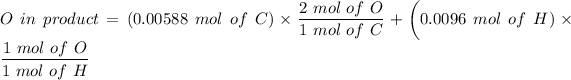
O in product = 0.02136 mol of O
∴
we are meant to divide the moles of each compound by the smallest number of moles; we have:
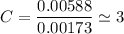
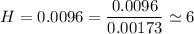
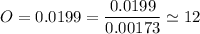

Thus; the empirical formula =
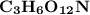
To estimate the molecular formula; we have:
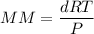

MM = 272.86 g/mol
Also; the molar mass of
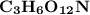 = 248 g/mol
= 248 g/mol
∴
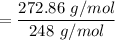
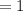
Thus; we can conclude that empirical formula as well as the molecular formula are the same.