Answer:
Velocity in the smaller pipe should not be included as an additional variable.
Step-by-step explanation:
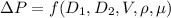
The dimensional formula of the variables are

Now using Buchingham's Pi Theorem, 6 - 3 = 3 dimensional parameters are required.
Use, D_1, V, \mu as the repeating variables.
Therefore,
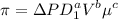

From this
1+c=0
-2+a+b-2c=0
-b+c=0
c=-1, b = -1, a = 1
Now,
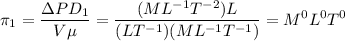
For

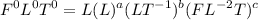
c = 0
1 + a + b - 2c = 0
-b + c = 0
Therefore, a = -1, b = 0, c = 0
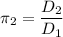
For
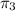


1 + c = 0
-4 + a + b - 2c = 0
2-b+c=0
c=-1, b=1, a = 1
Therefore,

Now checking,
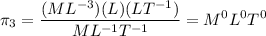
Therefore,
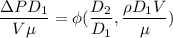
From continuity equation
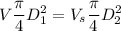
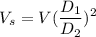
 is not independent of
is not independent of
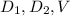
Therefore it should not be included as an additional variable.