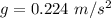Question

Communications satellites are placed in a circular orbit where they stay directly over a fixed point on the equator as the earth rotates. These are called geosynchronous orbits. The altitude of a geosynchronous orbit is

Answer 1

Complete Question

Communications satellites are placed in a circular orbit where they stay directly over a fixed point on the equator as the earth rotates. These are called geosynchronous orbits. The altitude of a geosynchronous orbit is 3.58×107m(≈22,000miles).

Part A

What is the period of a satellite in a geosynchronous orbit?

Part B

Find the value of g at this altitude.

Answer:

Part A

the period of a satellite in a geosynchronous orbit is 24 hours

Part B

the value of g at this altitude is
`g = 0.224 \ m/s^2`

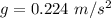
Step-by-step explanation:

From the question we are told that

The altitude of the geosynchronous orbit is
`r = 3.58* 10^7 \ m`

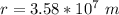
Generally 24 hr make up a day , which means that in 24 hours the earth does a complete rotation about its axis

Now from the question we are told that communications satellites are placed in a circular orbit where they stay directly over a fixed point on the equator as the earth rotate.it then means that the communications satellites has the same time period as the earth given that it is in a fixed position with respect to the earth

Generally the value of g at this altitude is mathematically represented as

`g = (G * M )/((R + r )^2)`

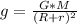
Here G is the gravitational constant with value
`G = 6.67 *10^(-11) \ N \cdot m^2 \cdot kg^2`

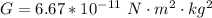
also M is the mass of the earth with value
`M = 5.97 *10^(24) \ kg`

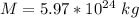
and R is the radius of the earth with value
`R = 6.38 *10^(6) \ m`

`g = (6.67*10^(-11) * 5.97*10^(24) )/(( 6.38*10^(6) + 3.58*10^(7) )^2)`

=>
`g = 0.224 \ m/s^2`