Question

Temperature: The temperature in Coldspot is -7° and is increasing 2.5° per hour. The temperature in Frostberg is 19° and is decreasing 4° per hour. How long will it be until the temperatures are the same? Write and solve an equation the represents the scenario.

Answer 1

It will be 4 hours until the temperatures are the same

Explanation:

Let
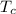`T_(c)` represent the temperature in Coldspot in
`x` hours and

`T_(f)` represent the temperature in Frostberg in
`x` hours.

From the question,

The temperature in Coldspot is -7° and is increasing 2.5° per hour, then we can write that

`T_(c) = -7 + 2.5x`

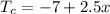
Also, from the question,

The temperature in Frostberg is 19° and is decreasing 4° per hour, then we can write that

`T_(f) = 19 - 4x`

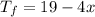
To determine how long it will be until the temperatures are the same, that is when
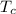`T_(c)` will be equal to
`T_(f)`, we will equate the two equations and determine
`x`.

`x` will give the number of hours until the temperatures are the same.

`T_(c) = T_(f)`

`-7 + 2.5x = 19 - 4x`

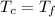
Then,

`4x + 2.5x = 19 + 7`

`6.5x = 26`

`x = (26)/(6.5)`

∴
`x = 4`

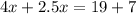
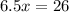
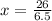
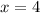
Hence, it will be 4 hours until the temperatures are the same.