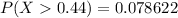Question

asked Dec 25, 2021 48.7k views

1 Answer

Liya · Answer 1 · 2021-12-29T21:54:38+0000

Complete Question

Given a population where the probability of success is p= 0.40 calculate the probabilities below if a sample of 300 is taken.

A. Calculate the probability the proportion of successes in the sample will be less than 0.42 (round 4 decimals)

B. What is the probability that the proportion of successes in the sample will be greater than 0.44 (round 4 decimals)

Answer:

A

P(X < 0.42) = 0.76028

B

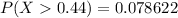
P(X > 0.44) = 0.078622

Explanation:

From the question we are told that

The probability of success is p = 0.40

The sample size is n = 300

Generally given that the sample size is large enough n > 30 then the mean for this sampling distribution is

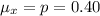
$\mu_(x) = p = 0.40$

Generally the standard deviation is mathematically represented as

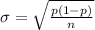
$\sigma = \sqrt{ (p (1 - p ))/(n) }$

=>
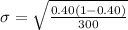
$\sigma = \sqrt{ (0.40 (1 - 0.40 ))/( 300) }$

=>
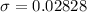
$\sigma = 0.02828$

Considering question A

Generally the probability the proportion of successes in the sample will be less than 0.42 is mathematically represented as

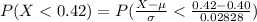
$P(X < 0.42) = P((X - \mu )/(\sigma ) < (0.42 - 0.40 )/( 0.02828) )$

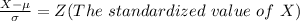
$(X -\mu)/(\sigma )  =  Z (The  \ standardized \  value\  of  \ X )$

=>
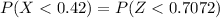
P(X < 0.42) = P(Z < 0.7072 )

From the z table

The area under the normal curve to the left corresponding to 0.7072 is

P(Z < 0.7072 ) = 0.76028

=>
P(X < 0.42) = 0.76028

Considering question B

Generally the probability the proportion of successes in the sample will be less than 0.44 is mathematically represented as

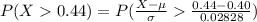
$P(X > 0.44) = P((X - \mu )/(\sigma ) > (0.44 - 0.40 )/( 0.02828) )$

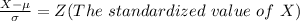
$(X -\mu)/(\sigma )  =  Z (The  \ standardized \  value\  of  \ X )$

=>
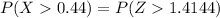
P(X > 0.44) = P(Z > 1.4144 )

From the z table

The area under the normal curve to the left corresponding to 1.4144 is

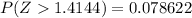
P(Z > 1.4144 ) = 0.078622

=>
P(X > 0.44) = 0.078622

Please log in or register to add a comment.