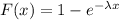Question

he time between arrivals of small aircraft at a county airport is exponentially distributed with a mean of one hour. Round the answers to 3 decimal places. (a) What is the probability that more than three aircraft arrive within an hour

Answer 1

The answer is below

Explanation:

The time between arrivals of small aircraft at a county airport is exponentially distributed with a mean of one hour. Round the answers to 3 decimal places.

(a) What is the probability that more than three aircraft arrive within an hour?

(b) If 30 separate one-hour intervals are chosen, what Is the probability that no interval contains more than three arrivals?

(c) Determine the length of an interval of time (in hours) such that the probability that no arrivals occur during the interval is 0.1.

Solution:

a) A poisson distribution is given by the formula:

`P(X=x)=(e^(-\lambda )\lambda^x)/(x!)`

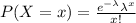
λ = 1 hour

Therefore:

P(X > 3) = 1 - P(X < 3) = 1 - [P(X = 0) + P(X = 1) + P(X = 2) + P(x = 3)]

`P(X=0)=(e^(-1)*1^0)/(0!)=0.3679`

`P(X=1)=(e^(-1)*1^1)/(1!)=0.3679`

`P(X=2)=(e^(-1)*1^2)/(2!)=0.1839`

`P(X=3)=(e^(-1)*1^3)/(3!)=0.0613`

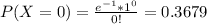
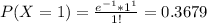
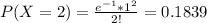
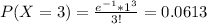
P(X > 3) = 1 - [0.3679+0.3679 + 0.1839 + 0.0613] = 0.019

b) Assuming 30 1 hour intervals, hence:

`P(X \leq 3)^(30)=[1-P(X\geq 30)]^(30)=(1-0.019)^(30)=0.5624`

c) mean = 1 hour

mean = 1 / λ

1 = 1 / λ

λ = 1

The cumulative distribution function of a continuous variable is:

`F(x)=1-e^(-\lambda x)`

`0.1=1-F(x)\\\\0.1=1-(1-e^(- x))\\\\0.1=e^(- x)\\\\-x=ln(0.1)\\\\-x = -2.3\\\\x=2.3\ hours`