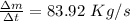Question

If the rocket has an initial mass of 6300 kg and ejects gas at a relative velocity of magnitude 2000 m/s , how much gas must it eject in the first second to have an initial acceleration of 27.0 m/s2 .

Answer 1

The amount of gas that is to be released in the first second in other to attain an acceleration of 27.0 m/s2 is

`(\Delta m)/(\Delta t) = 83.92 \ Kg/s`

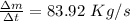
Step-by-step explanation:

From the question we are told that

The mass of the rocket is m = 6300 kg

The velocity at gas is being ejected is u = 2000 m/s

The initial acceleration desired is
`a = 27.0 \ m/s`

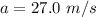
The time taken for the gas to be ejected is t = 1 s

Generally this desired acceleration is mathematically represented as

`a = (u * (\Delta m)/(\Delta t) )/(M -(\Delta m)/(\Delta t)* t)`

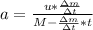
Here
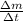`(\Delta m)/(\Delta t )` is the rate at which gas is being ejected with respect to time

Substituting values

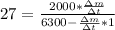
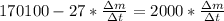
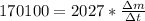
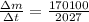
`27 = (2000 * (\Delta m)/(\Delta t) )/(6300 -(\Delta m)/(\Delta t)* 1)`

=>
`170100 -27* (\Delta m)/(\Delta t) = 2000 * (\Delta m)/(\Delta t)`

=>
`170100 = 2027 * (\Delta m)/(\Delta t)`

=>
`(\Delta m)/(\Delta t) = (170100)/(2027)`

=>
`(\Delta m)/(\Delta t) = 83.92 \ Kg/s`