Question

Mean birthweight is studied because low birthweight is an indicator of infant mortality. A study of babies in Norway published in the International Journal of Epidemiology shows that birthweight of full-term babies (37 weeks or more of gestation) are very close to normally distributed with a mean of 3600 g and a standard deviation of 600 g. Suppose that Melanie is a researcher who wishes to estimate the mean birthweight of full-term babies in her hospital. What is the minimum number of babies should she sample if she wishes to be at least 90% confident that the mean birthweight of the sample is within 225 grams of the the mean birthweight of all babies

Answer 1

Answer: 20

Explanation:

Formula to find the minimum sample size(n) when prior population standard deviation
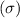`(\sigma)` is known.

`n=((z^c*\sigma)/(E))^2`, where E = Margin of error ,
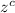`z^c`= Critical z-value for c confidence interval.

Given : E = 225 g ,
`\sigma=600` g

Critical z value for 90% confidence = 1.645

Now,
`n=((1.645*600)/(225))^2`

`n=((987)/(225))^2`

`n=(4.38666666667)^2=19.2428444\approx20`

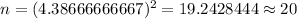
Hence, the required minimum sample size = 20