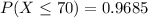Answer:
The probability is
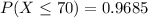
Explanation:
From the question we are told that
The mean values is
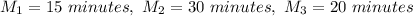
The standard deviation is
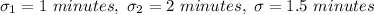
Generally the total mean is mathematically represented as
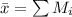
=>
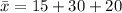
=>
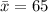
Generally the total variance is mathematically represented as
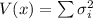
=>
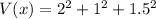
=>
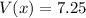
Generally the total standard deviation is mathematically represented as
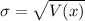
=>
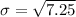
=>
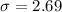
Generally the probability that it takes at most 70 min of machining time to produce a randomly selected component is mathematically represented as
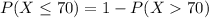
Here

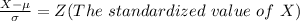
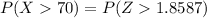
From the z table
The area under the normal curve to the right corresponding to 1.8587 is
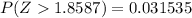
So

=>