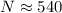Question

ore than 80 ml, and that the total pressure drop across the fibers should be no more than 105 dyne/cm2 at a total flow rate of 50 ml/s. If the blood viscosity is 3.5 cP and the density of blood is 1.05 g/cm3 , how many fibers should be used, and of what diameter should they be, so as to meet the design conditions

Answer 1

Complete Question

The complete question is shown on the first uploaded image

Answer:

The number of fibers is
`N \approx 540`

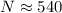
Step-by-step explanation:

From the question we are told that

The length of the fibers is
`L = 30 \ cm = 300 \ mm`

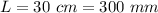
The hold up volume is
`V = 80 \ mL =0.08 L = 0.08 *10^(6)\ mm^3`

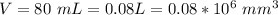
The total pressure that must not be exceeded
`P_t = 10^5 \ dync/cm^2`

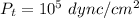
The total flow rate is
`\r m = 50 ml/s = 0.05 \ l/ s = 0.05 *10^(6) \ mm^3 /s`

The blood viscosity is
`\eta = 3.5\ cP = 0.0035\ kg \cdot s^(-1) \cdot m^(-1) = 0.0035 *10 = 0.035 \ kg \cdot s^(-1 ) \cdot cm^(-1)`

The density of the blood is
`\rho = 1.05 \ g/cm^3`

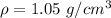
Generally the volume of blood a single fiber can contain at a time is mathematically represented as

`V = (\pi)/(4) * d^2 * L`

Here diameter of the fiber

So

`d = \sqrt{(4 V)/(\pi * L)}`

=>
`d = \sqrt{(4 * 0.08 *10^(6) )/(3.142 * 300)}`

=>
`d = 18.42 \ mm`

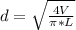
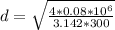
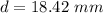
Converting to cm

=>
`d = 18.42 * 10 = 1.842 \ cm`

Generally the pressure in the fiber is mathematically represented as

`P = (32 * \eta * \r v * L )/( d^2 )`

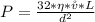
Generally the velocity of the blood flow which is mathematically represented as

`\r v = ( 4 *0.05 *10^(6) )/(3.142 * 18.42 )`

=>
`\r v = 187.62 \ mm/s`

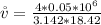
Converting to cm

=>
`\r v = (187.62 )/(10) = 18.762 \ cm/s`

So

`P = (32 * 0.035 * 18.76 * 30 )/( 1.842^2 )`

=>
`P = 185.77 \ dync / cm^2`

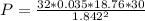
Generally the number of fibers required is mathematically represented as

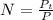
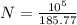
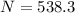
`N = (P_t)/(P)`

=>
`N = (10^5)/(185.77)`

=>
`N = 538.3`

=>
`N \approx 540`