Question

In a double-slit experiment the distance between slits is 5.6 mm and the slits are 0.81 m from the screen. Two interference patterns can be seen on the screen: one due to light of wavelength 410 nm, and the other due to light of wavelength 660 nm. What is the separation in meters on the screen between the m

Answer 1

The separation in meters on the screen between the bright fringes of the two interference patterns is 1.08 × 10⁻⁴ m

Step-by-step explanation:

Here is the complete question:

In a double-slit experiment, the distance between slits is 5.6 mm and the slits are 0.18 m from the screen. Two interference patterns can be seen on the screen: one due to light of wavelength 410 nm, and the other due to light of wavelength 660 nm. What is the separation in meters on the screen between the third-order (m = 3) bright fringes of the two interference patterns?

Step-by-step explanation:

For a bright fringe, the distance
`y` of the bright fringe can be determined from

`y =(m\lambda D)/(d)`

Where
`m` is the order

`\lambda` is the wavelength

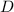`D` is the distance from the screen

`d` is the distance between the slits

From the question,

`d` = 5.6 mm = 5.6 × 10⁻³ m

`D` = 0.81 m

m = 3

For the first interference pattern,
`\lambda` = 410 nm = 410 × 10⁻⁹ m

∴
`y =(m\lambda D)/(d)` becomes

`y =(3 * 410 * 10^(-9) * 0.81)/(5.6 * 10^(-3) )`

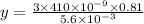
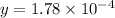`y = 1.78 * 10^(-4)` m

For the second interference pattern,
`\lambda` = 660 nm = 660 × 10⁻⁹ m

∴
`y =(3 * 660 * 10^(-9) * 0.81)/(5.6 * 10^(-3) )`

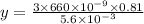
`y = 2.86 * 10^(-4)` m

Now, the separation between the bright fringes of the two interference patterns will be the difference in the distances of the bright fringes for the two interference patterns. That is

2.86 × 10⁻⁴ m - 1.78 × 10⁻⁴ m = 1.08 × 10⁻⁴ m

Hence, the separation in meters on the screen between the bright fringes of the two interference patterns is 1.08 × 10⁻⁴ m.