Question

Suppose that the average number of new clients that a sales representative signs in a month is 22 and that the distribution of this random variable is Poisson. What is the probability that any given sales representative will sign fewer than 15 new clients in a month

Answer 1

Answer: 0.04769

Explanation:

Let the average number of new clients that a sales representative signs in a month be
`\lambda`.

Given:
`\lambda=22`

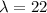
Poisson distribution formula:

`P(X=x)=(e^(-\lambda)\lambda^x)/(x!)`

The probability that any given sales representative will sign fewer than 15 new clients in a month = P(X<15)

`=\sum^(14)_(x=0)(e^(-22)(22)^x)/(x!)\approx0.04769\ [\text{By Poisson distribution table}]`

Hence, the probability that any given sales representative will sign fewer than 15 new clients in a month =0.04769