Answer:
The number
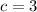 satisfies the conclusion of Rolle's Theorem for
satisfies the conclusion of Rolle's Theorem for
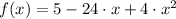 .
.
Explanation:
According to the Rolle's Theorem, for all function continuous on
![[a,b]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/dyyh30s5r4ox0wg76shisxuulr9zptlacg.png) , there is a value
, there is a value
 (
(
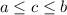 ) such that:
) such that:
 (Eq. 1)
(Eq. 1)
Where:
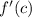 - First derivative of the function evaluated at
- First derivative of the function evaluated at
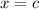 , dimensionless.
, dimensionless.
 ,
,
 - Lower and upper bounds, dimensionless.
- Lower and upper bounds, dimensionless.
 ,
,
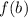 - Function evaluated at lower and upper bounds, dimensionless.
- Function evaluated at lower and upper bounds, dimensionless.
Let
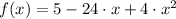 , then upper and lower values are, respectively:
, then upper and lower values are, respectively:
Lower bound (
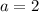 )
)
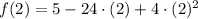

Upper bound (
 )
)
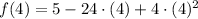
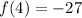
From Rolle's Theorem, we find that first derivative evaluated at
 is:
is:

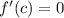
Then, we find the first derivative of the function, equalize
 to
to
 and solve the resulting expression:
and solve the resulting expression:
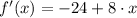
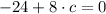
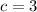
The number
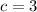 satisfies the conclusion of Rolle's Theorem for
satisfies the conclusion of Rolle's Theorem for
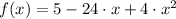 .
.