Question

Tutoring Services: The Community College Survey of Student Engagement reports that 46% of the students surveyed rarely or never use peer or other tutoring resources. Suppose that in reality 40% of community college students never use tutoring services available at their college. In a simulation we select random samples from a population in which 40% do not use tutoring. For each sample we calculate the proportion who do not use tutoring. If we randomly sample 500 students at a time, what will be the mean and standard error of the sampling distribution of sample proportions

Answer 1

Answer: Mean = 0.40 and standard error = 0.0219 of the sampling distribution of sample proportions.

Explanation:

Given : The proportion of community college students never use tutoring services available at their college: p= 0.40

Mean of the sampling distribution of sample proportions = p = 0.40

Since sample size : n= 500

Standard error =
`\sqrt{(p(1-p))/(n)}=\sqrt{(0.40(1-0.40))/(500)}`

`=\sqrt{(0.24)/(500)}`

`=√(0.00048)=0.0219`

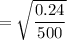
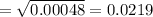
Hence, Mean = 0.40 and standard error = 0.0219 of the sampling distribution of sample proportions.