Question

3.a. Solve the following equations.
​

Answer 1

1. Solving
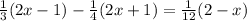`(1)/(3)(2x-1)-(1)/(4)(2x+1)=(1)/(12)(2-x)` we get x=3

2. Solving
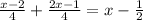`(x-2)/(4)+(2x-1)/(4)=x-(1)/(2)` we get x=-1

Explanation:

We need to solve the equations:

1.
`(1)/(3)(2x-1)-(1)/(4)(2x+1)=(1)/(12)(2-x)`

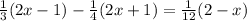
Expanding the brackets

`(2x)/(3)-(1)/(3) -(2x)/(4)-(1)/(4) =(2)/(12)-(x)/(12) \\(2x)/(3)-(1)/(3) -(x)/(2)-(1)/(4) =(1)/(6)-(x)/(12)`

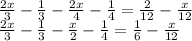
Taking LCM on left side we get 12

`(2x*4-1*4-x*6-1*3)/(12)= (1)/(6)-(x)/(12)\\(8x-4-6x-3)/(12)= (1)/(6)-(x)/(12)\\(8x-6x-3-4)/(12)= (1)/(6)-(x)/(12)\\(2x-7)/(12)= (1)/(6)-(x)/(12)\\(2x)/(12)-(7)/(12)= (1)/(6)-(x)/(12)`

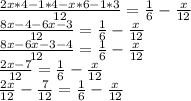
Add 7/12 on both sides

`(2x)/(12)-(7)/(12)+(7)/(12) = (1)/(6)-(x)/(12)+(7)/(12)\\(x)/(6)=(1*2-x+7)/(12)\\ (x)/(6)=(-x+9)/(12) \\(x)/(6)=-(x)/(12) +(9)/(12)\\ (x)/(6)=-(x)/(12) +(3)/(4)`

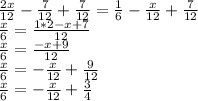
Adding x/12 on both sides and simplifying

`(x)/(6)+(x)/(12) =-(x)/(12) +(3)/(4)+(x)/(12)\\(x*2+x)/(12)=(3)/(4)\\(3x)/(12)= (3)/(4)\\`

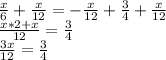
Multiply both sides by 12/3

`(3x)/(12)*(12)/(3)=(3)/(4)*(12)/(3) \\Simplifying:\\x=3`

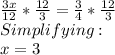
So, solving
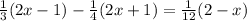`(1)/(3)(2x-1)-(1)/(4)(2x+1)=(1)/(12)(2-x)` we get x=3

2.
`(x-2)/(4)+(2x-1)/(4)=x-(1)/(2)`

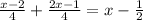
Taking LCM and solving:

`(x-2+2x-1)/(4)=(2x-1)/(2)\\(x+2x-1-2)/(4)=(2x-1)/(2)\\(3x-3)/(4)=(2x-1)/(2)\\`

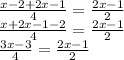
Cross multiplying

`2(3x-3)=4(2x-1)\\6x-6=8x-4\\Combining\ like\ terms \ :\\6x-8x=-4+6\\-2x=2\\x=-1`

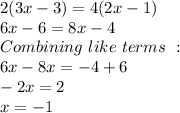
So, solving
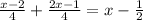`(x-2)/(4)+(2x-1)/(4)=x-(1)/(2)` we get x=-1