Answer:
810 cm^3
Explanation:
Since,the l(length) b(breadth) & h(height) of the cuboid bear the ratio 5 : 3 : 2 ,we could assume it as:
We know that,
- Cuboid ( total surface area)= 2lb+2lh+2hb cubic units
So substitute the dimensions we assumed:
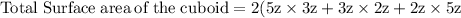
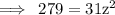
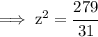
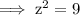
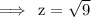
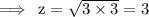
Hence, according to the formula,
We got the dimensions of the cuboid, i.e.
Then, solve.
- Cuboid V = lbh
- 15 cm * 9 cm * 6 cm
- 810 cm^3
Hence,the volume of the cuboid will be 810 cm^3