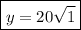Answer:
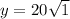
Explanation:
The construction of the figure gives us three right triangles, where we can apply Pythagora's Theorem.
I have added two variables to the image in the picture attached.
On the triangle with sides y,h,16 we have:
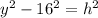
On the triangle with sides h,z,25 we have:
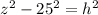
Equating
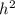 :
:
![y^2-16^2=z^2-25^2\qquad\qquad [1]](https://img.qammunity.org/2021/formulas/mathematics/college/tvyntgawmew7dzap08spkgcx9lznudcr49.png)
On the bigger triangle with sides y,z,16+25=41 we have:
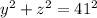
Adding this last equation with [1]:
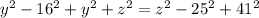
Simplifying:
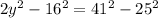
Operating:
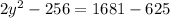
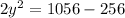
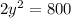
Dividing by 2:
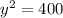
Taking square root:
y=20
To enter the number in the required format: