Question

8. The graph below shows a dashed line on a coordinate plane. A right triangle is drawn so

that the side opposite of the right angle lies on the dashed line.
(5, -3)
(13,-9)
Which right triangle has a side opposite the right angle with a slope that would lie on the
dashed line shown in the graph? (NOTE: Triangles may not be drawn to scale or proper
orientation)

Answer 1

Option 2

Explanation:

First, find the slope of the line of the graph using the points given as (5, -3) and (13, -9):

`slope = (y_2 - y_1)/(x_2 - x_1) = (-9 -(-3))/(13 - 5) = (-6)/(8) = -(3)/(4)`

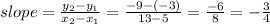
Any of the triangle in the options given, whose opp side has the same slope value of -¾, is the triangle we are looking for.

Option 1: slope between the points (0, 2) and (3, -2).

`slope = (y_2 - y_1)/(x_2 - x_1) = (-2 - 2)/(3 - 0) = (-4)/(3)`

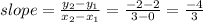
Option 2: slope between the point (-7, 6) and (-3, 3).

`slope = (y_2 - y_1)/(x_2 - x_1) = (3 - 6)/(-3 -(-7)) = (-3)/(4)`

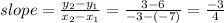
Option 2 has the same slope as the one given in the graph. This is the answer.

Option 3: slope between the points (5, -1) and (2, -5).

`slope = (y_2 - y_1)/(x_2 - x_1) = (-5 -(-1))/(2 - 5) = (-4)/(-3) = (4)/(3)`

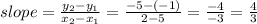
Option 4: slope between the points (2, -7) and (6, -4).

`slope = (y_2 - y_1)/(x_2 - x_1) = (-4 -(-7))/(6 - 2) = (3)/(4) = (3)/(4)`

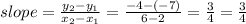
The answer is Option 2