Question

Consider the series
`(1)/(4) +(1)/(3) +(4)/(9) +(16)/(27) +(64)/(81)`

Does the series converge or diverge?

Answer 1

The given series can be condensed to

`\displaystyle \frac14 + \frac13 + \frac49 + (16)/(27) + (64)/(81) + \cdots = \frac14 \left(1 + \frac43 + (4^2)/(3^2) + (4^3)/(3^3) + \cdots\right) = \frac14 \sum_(n=0)^\infty \left(\frac43\right)^n`

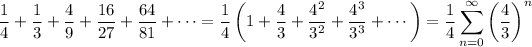
which is a geometric series with ratio 4/3. Since this ratio is larger than 1, the sequence of partial sums of the series diverges, so the infinite series also diverges.

We can also just the n-th term test:

`\displaystyle \lim_(n\to\infty) \frac14 \left(\frac43\right)^n = \frac14 \lim_(n\to\infty) (4^n)/(3^n) = \infty`

since 4ⁿ > 3ⁿ for all n > 0.

Answer 2

Diverge

Explanation:

Each successive term is larger than the previous one, so the series will diverge.