Question

Please help!

20 points possible!

Answer 1

1) See Attachment.

2) The slope is -2/3.

3) The y-intercept is y=2.

Explanation:

We have the two points (6, -2) and (-3, 4) and we know that they are on the same line.

Part 1)

In order to graph a line given two points, we simply need to plot those two points and then draw a line through them.

Please see the attachment.

We would plot (6, -2) and (-3, 4). Then, use a straightedge to connect the two points.

Part 2)

To find the slope, we can use the slope formula.

The slope formula for the slope between any two points is:

`m=(y_2-y_1)/(x_2-x_1)`

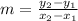
Where (x₁, y₁) and (x₂, y₂) are our two points.

So, let‘s let (6, -2) be (x₁, y₁) And (-3, 4) be (x₂, y₂). Substituting them into the slope formula yields:

`m=(4-(-2))/(-3-6)`

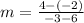
Evaluate:

`m=(6)/(-9)=-2/3`

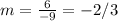
So, the slope is -2/3.

We can confirm this using our graph. Remember that the slope measures rise over run.

We are going down by 2 for every 3 to the right.

Part 3)

The y-intercept is where the graph crosses the y-axis.

From the graph, we can see that the graph crosses the y-axis at (0, 2).

Therefore, the y-intercept is y=2.