Question

What is the factored form of the function f(x)=x^3+8x^2+5x−50?

Answer 1

the factors of f(x)=x^3+8x^2+5x-50 are (x-2)(x+5)(x+5)

Explanation:

We need to factorise the function
`f(x)=x^3+8x^2+5x-50`

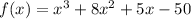
If a number is a factor of this function than it must be completely divisible by last co-efficient. Our last co-efficient is -50

Checking few numbers:

`f(1)=(1)^(3)+8(1)^2+5(1)-50\\f(1)=1+8+5-50\\f(1)=-32\\Now \ putting \ x= 2 \\f(2)=(2)^(3)+8(2)^2+5(2)-50\\f(2)=8+8(4)+10-50\\f(2)=8+32+10-50\\f(2)=0`

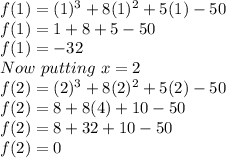
So, f(2)=0 which means x-2 is a factor of the given function. Now we will perform long division of
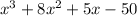`x^3+8x^2+5x-50` by (x-2) to find other factors

The long division is shown in figure attached.

After long division we get:
`x^2+10x+25`

The equation
`x^2+10x+25` can be further simplified as: (x+5)(x+5) or (x+5)^2

So, the factors of f(x)=x^3+8x^2+5x-50 are (x-2)(x+5)(x+5)