Hello,
As 2a and b are two distinct roots of P(x) we can write the following:
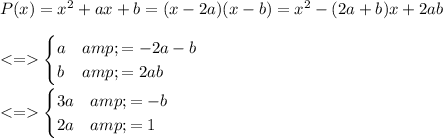
Then, a=1/2 and b=-3/2
a+b=1/2-3/2=-1
thanks
Actually, we cannot simplify by b if b is different from 0 so we should take into account the specific case of b=0 but then we come up with a=-2a so a=0 and then 2a=0 et b=0 and this is not possible because it says that 2a and b are two distinct roots, so the case where b=0 is not possible so we can assume that b is different from 0 and then we can simplify b=2ab by 1=2a, so we are good. the solution is a+b=-1