Question

A parallel–plate capacitor has circular plates of 8.2 cm radius and 1.3mm separation. (i) Calculate the capacitance. (ii) What charge will appear on the plates if a potential difference of 120V is applied? (b) A 2.0μF spherical capacitor is composed of two metal spheres, one having a radius twice as large as the other. If the region between the spheres is a vacuum, determine the volume of this region.​

Answer 1

Hello!

(i)

Recall the equation for the capacitance of a parallel-plate capacitor:

`C = (\epsilon_0 A)/(d)`

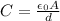
C = Capacitance (F)
ε₀ = Permittivity of Free Space (8.85 × 10⁻¹² C²/Nm²)

A = Area of each plate (A = πr² = π(0.082²) = 0.0211 m²)
d = separation between plates (0.0013m)

Plug in the values to solve.

`C = ((8.85 * 10^(-12))(0.0211))/(0.0013) = 1.4387 * 10^(-10) F = \boxed{0.14387 nF}`

(ii)
Using the following equation:

`C = (Q)/(V)`

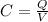
Q = Charge on capacitor (C)

V = Potential difference of capacitor (V)
Rearrange to solve for charge and solve.

`Q = CV\\\\Q = (1.4387* 10^(-10)) (120) = 1.7265 * 10^(-8) C = \boxed{17.265nC}`

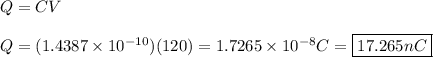
**Remember that NEITHER charge OR voltage affects the capacitance; capacitance is STRICTLY determined by geometry.

(B)
We can begin by deriving the equation of the capacitance of a two-sphere spherical capacitor using the following:

`C = (Q)/(|\Delta V|)`

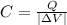
We know that:

`\Delta V = -\int E \cdot dr`

Let's say that the inner sphere's radius is 'r', and the outer sphere's radius is '2r'. These are our limits for the integral. The electric field of a spherical charge is given as:

`E = (kQ)/(r^2)`

Now, we can integrate to find the potential difference between the two spheres.

`\Delta V = -\int\limits^(2r)_r {(kQ)/(r^2)} \, dr\\\\\Delta V = (kQ)/(r)\left \| {{2r} \atop {r}} \right. \\\\\Delta V = (kQ)/(2r) - (kQ)/(r) = -(kQ)/(2r)\\\\ |\Delta V| = (kQ)/(2r)`

Using the equation for capacitance:

`C = (Q)/((kQ)/(2r))\\\\C = (2r)/(k)`

Solve for 'r'. Recall that k = 8.99 × 10⁹ Nm²/C².

`r = (Ck)/(2) = ((0.000002)(8.99* 10^9))/(2) = 8990 m`

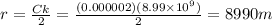
Since the radius of the outer is '2r', we can easily solve for the outer sphere's radius and subtract the volume of the inner from the outer to find the volume of the region between the spheres.

`V_(outer) = (4)/(3)\pi (17980^2) = 1354153772.92 m^3\\\\V_(inner) = (4)/(3)\pi (8990^2) = 338538443.23 m^3\\\\V_(outer) - V_(inner) = 1015615329.69 m^3 = \boxed{1.0156 * 10^9 m^3}`