Answer:
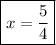
Explanation:
Solve for the value of
 :
:
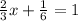
-Subtract
 to both sides and convert the
to both sides and convert the
 into a fraction. Since they both fractions
into a fraction. Since they both fractions
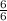 and
and
 both have the same denominators, then you would subtract the numerators:
both have the same denominators, then you would subtract the numerators:
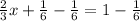
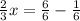

-Multiply both sides by
 which is the reciprocal of
which is the reciprocal of
 . By multiplying two you need to multiply both numerators and denominators:
. By multiplying two you need to multiply both numerators and denominators:

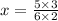
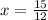
-Simplify the fraction by reducing by
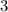 :
:
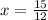
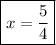
Therefore, the value of
 is
is
 .
.