Question

What’s the distance between (-5 , 1) and (2, 4)

Answer 1

`\boxed {d = √(58)}`

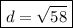
Explanation:

Use the Distance Formula to help determine the distance between the two given points:

`d = \sqrt{(x_(2) - x_(1)) ^(2) + (y_(2) - y_(1))^(2)}`

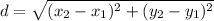
First point:
`(x_(1), y_(1))`

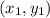
Second point:
`(x_(2), y_(2))`

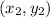
-Apply the given points onto the formula:

First point:
`(-5, 1)`

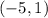
Second point:
`(2, 4)`

`d = \sqrt{(2 + 5) ^(2) + (4 - 1)^(2)}`

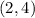
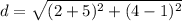
-Solve for the distance:

`d = \sqrt{(2 + 5) ^(2) + (4 - 1)^(2)}`

`d = \sqrt{(7) ^(2) + (3)^(2)}`

`d = √(49 + 9)`

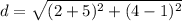
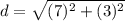
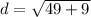
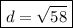`\boxed {d = √(58)}` (since the number can't be square rooted, it will stay written the same)

Therefore, the distance is
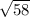`√(58)`.